Топология и запутанность — два мощных принципа для характеристики структуры сложных квантовых состояний. В новой статье в журнале Physical Review X исследователи из Пенсильванского университета устанавливают связь между ними.
«Наша работа объединяет две большие идеи, — говорит Чарльз Кейн, почетный профессор физики Кристофера Х. Брауна в Школе искусств и наук Пенна. «Это концептуальная связь между топологией , которая представляет собой способ характеристики универсальных свойств, которыми обладают квантовые состояния, и запутанностью, которая представляет собой способ, которым квантовые состояния могут демонстрировать нелокальные корреляции, когда что-то, что происходит в одной точке пространства, коррелирует с чем-то, что происходит в другой части пространства. То, что мы обнаружили, представляет собой ситуацию, когда эти понятия тесно переплетены».
Семя для изучения этой связи пришло во время долгих часов, которые Кейн провел в своем домашнем офисе во время пандемии, обдумывая новые идеи. Один из ходов мыслей заставил его представить классическое изображение из учебника поверхности Ферми меди, которая представляет собой потенциальную энергию электронов металла. Это картина, которую видит каждый студент-физик, и Кейн был хорошо знаком с ней.
«Конечно, я узнал об этом изображении еще в 1980-х годах, но никогда не думал, что оно описывает топологическую поверхность, — говорит Кейн.
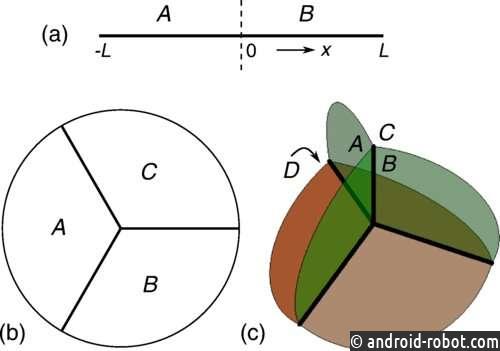
Классический способ осмысления топологических поверхностей, по словам Кейна, состоит в том, чтобы рассмотреть разницу между пончиком и сферой. Какая разница? Единственная дыра. Топология рассматривает эти обобщаемые свойства поверхности, которые не изменяются при деформации. В соответствии с этим принципом кофейная чашка и пончик будут обладать одним и тем же топологическим свойством.
Если рассматривать поверхность Ферми меди как топологический объект, то соответствующее количество дырок, которыми она обладает, равно четырем, цифра, также известная как род. Как только Кейн начал думать о поверхности Ферми таким образом, он задался вопросом, может ли существовать связь между родом и квантовой запутанностью.
Для дальнейшего исследования этой потенциальной связи Кейн привлек своего аспиранта Пока Мана Тама и Мартина Клаассена, доцента физики Пенсильванского университета, который в своей работе сосредоточился на квантовой запутанности. Вместе они вывели математическую связь между родом поверхности Ферми и мерой квантовой запутанности, называемой взаимной информацией. Взаимная информация характеризует корреляции, которые могут возникать в разрозненных областях пространства, встречающихся в одной точке. Число, известное как характеристика Эйлера, тесно связанное с родом, обеспечило точную связь между ними.
Исследователи установили, что связь между топологией и запутанностью существует в простой металлической системе, где электроны движутся независимо друг от друга, а затем расширили свой анализ, чтобы показать, что связь также присутствует, даже когда электроны взаимодействуют с большей сложностью.
И хотя теоретическая работа была проделана на металлах, Кейн считает, что она будет распространяться и на другие материалы, такие как те, которые связаны с очень сильным взаимодействием между электронами.
«Это может позволить нам разработать новые способы мышления о фазах материи, которые мы не очень хорошо понимаем и у которых не так много инструментов для исследования», — говорит Кейн. «Люди пытаются выяснить, как использовать квантовую механику , чтобы воспользоваться квантовой информацией. Чтобы сделать это, вы должны понять, как проявляется квантовая механика, когда у вас есть много степеней свободы. Это очень сложная проблема, и это работа подталкивает нас в этом направлении».
В последующей работе Кейн и его коллеги надеются разработать эксперименты, которые продолжат исследовать вновь обнаруженную связь, возможно, разработав новую технику для измерения топологического рода и способ исследования структуры квантовой запутанности.